An intro to Quantum Physics, fixing the math in "the sequences"
Confidence level: I am a physicist with a phd in computational quantum chemistry. I’m pretty sure there are no major errors here, but I still may have missed something. Thanks to Blake Stacey for looking over the post.
The goal of this post is to rewrite everything in the three LessWrong posts “configurations and amplitudes”, “Joint configurations”, and “distinct configurations”. These are part of “the sequences”, a series of blog posts by Eliezer Yudkowsky that form the foundational text of the “Rationalist” subculture. I think they were noble attempts to explain a very difficult subject. Unfortunately, all of them are based on a mathematically incorrect description of their subject matter.
The first part of this post is a new introduction to the basics of quantum physics, using a basic interferometer setup as our guide. It is aimed at the dedicated layman level: There will be math, but it will be generally basic. The main aim is for you to get a feel for how things actually operate at the quantum level. It should cover all the material in those three posts above, but with corrected math and more useful explanations.
Only then, in the second part, will I explain why the original sequences are incorrect and deeply flawed. If you are just here for the drama, you can skip to the section “why the sequences posts are incorrect”.
Part 1: The quantum world
Introduction to amplitudes
At the smallest level, the universe is run by the rules of quantum physics, which are fundamentally unlike anything we encounter in our everyday life. A light photon is not a billiard ball, or a wave of water. It’s a third thing which shares characteristics of both or neither, and it acts in a new way, according to new rules.
The quantum world is described by a “wavefunction”, that allows us to calculate how likely any configuration of physical properties is to occur. Each possible configuration is assigned a “probability amplitude”, which is a complex number that is attached to that configuration of our system.
When talking about a configuration, I will place it in brackets |like this>1. For example, in the Schrodinger cat scenario, we could assign an amplitude of 0.1 + 0.2i to the configuration |cat is dead>, and and an amplitude -0.9 + 0.37i to the configuration |cat is alive>. Obviously, these amplitudes themselves are not probabilities (you can’t have a 0.6i probability of something happening), but they can be converted into probabilities. The actual probability of finding each configuration when measured is given by the absolute value of the amplitude squared (our cat above has a ~95% survival rate).
To better understand these probability amplitudes, let’s pretend there’s only one light photon in the world, travelling to the right. The amplitude of the configuration |a photon is heading to the right> is then given by the following equation2:
If you didn’t do advanced math in high school, you might be scared of the whole concept of exponentiating an imaginary number. but it’s actually fairly simple.
You can plot the real and imaginary parts of a complex number as an arrow on a 2d graph of real vs imaginary components, like the one below. What e^iθ does is draw an arrow on this graph that traces a circle. To calculate it’s value, you take an arrow of length 1 pointing right (the number 1 + 0i), and then rotate it counterclockwise by an angle of θ. You can then read the new number off the graph. (Fortunately, we will avoid the need for trigonometry in this article.)
You might have heard the famous equation e^iπ = -1. In this formulation, what this means is that when you rotate the arrow by an angle of pi radians (we are using radians here, where π = 180 degrees or half a circle), the arrow points to -1+0i = -1. In fact, no matter where the arrow is pointing, adding a half a circle of rotation will make it point in the opposite direction, which is the same as multiplying it by -1.
In our photon, the angle θ changes as the photon moves. The effect will be that after a certain distance, the arrow will have rotated around a bit and point in a new direction, leading to a new amplitude. This is why, in the following discussion, it’s very important that the total distance travelled by each light beam is exactly the same3. The rotation of the arrow by a certain angle is called a “phase shift”.
Earlier I said that the way to calculate probabilities from amplitudes was to take the absolute value squared. We can think of this as taking the length of the arrow, and squaring it, to get the likelihood of the particular state.
If our psi is e^iθ, this is very easy, because the length of this arrow is always 1, so we our probability of finding the photon is 1^2 = 1= 100%. So far so easy.
The interferometer
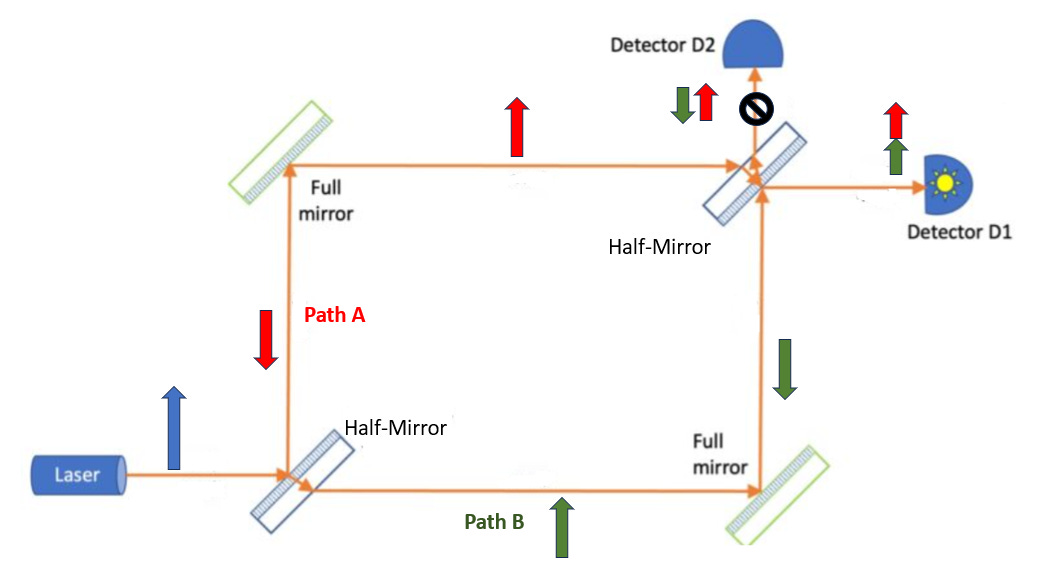
One photon on it’s own isn’t particularly interesting, so let’s introduce an experimental setup called an “interferometer”. It’s a system where a beam of light is split into two sections and then recombined with a series of mirrors. Only in this case, we are only firing a single photon.

To split the photon, we use a device called the “half-silver mirror”. The actual formal treatments of beam splitters requires a few math tools that aren’t worth explaining, and different beam splitters can have different setups, but for one photon on a simple half-silver mirror, the rule goes as follows:
When a half mirror is hit by part of a photon, the incoming beam is split into two separate configurations. One is “transmitted”, continuing forward, and one is “reflected”, changing direction. The amplitudes of both configurations is scaled down from the incoming amplitude by multiplying them by 1/√2 (around 0.71).
If (and only if) a beam has been reflected from the front side of a half-mirror, it also undergoes a phase shift, and is multiplied again by -1. This can be thought of as rotating our amplitude arrow by an extra half circle, or by flipping it to face the opposite direction. If it’s transmitted, or reflected from the back of a half mirror, no phase shift occurs. The reason it only happens from the front is due to the rules about transferring between different dielectric materials, and this phase shift rule is required for conservation of energy.
So now the probability amplitude of the photon now has two components, describing the two possible configurations of |photon is on path A> or |photon is on path B>. Each configuration has an amplitude arrow attached, which each point in opposite directions. Both amplitudes have length 1/√2. From now on, we’ll just keep track of relative phases, assuming they have gone the same distance. This also means we will not have to think about imaginary numbers for the rest of this article. So if the arrow was pointing up when it hit the mirror, then it’s pointing down in path A, but up in path B.
If you now put a detector in path A , it will find a photon with probability (1/√2 ^2 = 1/2), and same for path B. This means that there is a 50% chance of the configuration |photon in path A only>, and 50% chance of the configuration |photon in path B only>. The arrow direction still has no effect on the probability.
We call this a “superposition” of different configurations, because if you look, you will never find half a photon in either path. It will always be like the whole photon went this way or that way. This is why the photon cannot be only a wave: if it was, then you would be able to find “half photons”.
Next, both beams bounce off full mirrors and change direction. Since no splitting occurs, no scaling occurs either, but they do both undertake another phase shift of half a circle (multiply by -1). This doesn’t affect anything. After all, both light particles are constantly changing arrow direction, what matters is their relative phase. At this point, when they have travelled equal distance, they are still pointing in opposite directions.
Now, each of the beams hit the next half mirror, and things get interesting.
First, each of the 2 beams has been split again into 2, so we now have 4 new amplitudes to think about, for all the different paths of the light. The length of each will be 1/√2 times 1/√2 = 1/2.
At last, we get to the relevance of the arrow directions! If we say the path A amplitude is pointing up (at the point of mirror launch), then the path B amplitude is pointing down.
The path A beam (arrow pointing up) hits the back of the half-mirror (no phase shift), so it transmits one arrow into detector 1, pointing up, and reflects one arrow to detector 2, pointing up.
The path B beam (arrow pointing down) hits the front of the half mirror, so it transmits one arrow into detector 2, pointing down, and reflects one arrow to detector 1, which undergoes a phase shift of -1 and points up.
Now we get to the crux. Nature does not label photons, and does not care about their history. So, while bits of the photon have taken different paths, with different amplitudes, there are only two possible final configurations: Either there is a photon at detector 1 or a photon at detector 2. If two different paths lead to the same configuration, to figure out the amplitude of that configuration, you just add the amplitude of the contributing paths.
In detector 1, we get an up arrow and and a down arrow. To get the amplitude of the resulting configuration |photon went into detector 1>, we add them together. But since one is the negative of the other, they cancel out (“destructively interfere”), and add to 0.
In detector 2, we get two up arrows of length 1/2. To get the amplitude of the resulting configuration |photon went into detector 2>, they add together (constructively interfere), to produce a final amplitude arrow pointing up with length 1.
What is the probability of finding the photon in each detector? We square the length of the arrows, and you get 1^2 = 1 in the detector 2, and 0^2 = 0 in detector 1. So the result is that there is a 100% chance of finding the photon in detector 2, and no chance in detector 14.
So the photon has interfered with itself into nothing, like a wave. However, no matter what you do the detector never sees the photon energy “split” between detectors, like a particle. (We can do similar experiments with bulky things like electrons). To rescue the idea that it must be one or the other, you might propose that there are secret instructions in the photon telling it about what actions to take, that just so happen to end up at detector D1 for some reason. This can run into problems like the following:
Imagine if we put a block into one of the paths, and recalculated where the photons would end up:
The block cuts off the beam from path A, but allows path B through. Before the block, you would never find a photon in Detector 2, but now it shows up there in a quarter of experiments. (in another quarter of experiments, D1 will go off, and in the remaining half of experiments, the photon was blocked on path A)
But wait, a photon going through path B never saw path A! An obstacle in the path not travelled has affected the behavior of a photon in another path. You can take this further: you can place this blocker in the path after the initial split has happened (but before the alternate path would have hit it), and the result will be the same. This only really makes sense if the photon really is split in between the two paths in some way. There is no secret information in the photon that can know in advance whether you will place a block in the path not taken in the future.5
Two photon interference and joint configurations
So far we have only been looking at a single photon. But a large part of the weirdness of quantum mechanics occurs when we are looking at the interaction between different particles.
Again, we will use a half mirror, but this time, we send two photons in instead of one.
This might look similar to the second half-mirror in our interferometer example. But actually, the presence of an extra photon complicates things quite a bit. In our 1 photon example, we were going from a superposition of two possible configurations:
superposition of |photon in path A> and |photon in path B>
to another superposition of two possible configurations:
superposition of |photon in path D1> and |photon in path D2>
In our new case, we are going from the single configuration:
|one photon in path A and one photon in path B>
to a superposition of three possible configurations:
superposition of |there are 2 photons in D1> and |there is 1 photon in D1 and another in D2> and |there are 2 photons in D2>
This means you can’t quite use the same rules from earlier. We can say that each photon can either transmit or reflect when it hits the mirror. There are four paths (we’ll assume the incoming amplitudes are both 1, and we keep our rule that only reflection from the front induces phaseshift):
Both photons are reflected: state is |1 photon in D1, 1 photon in D2>, phase shift occurs,
amplitude -(1/2)
Photon A is transmitted, photon B is reflected: state is |2 photons in D1>, phase shift occurs, amplitude -(1/√2)
Photon A is reflected, photon B is transmitted: state is |2 photons in D2>, no phase shift, amplitude (1/√2)
Both photons are transmitted: state is |1 photon in D1, 1 photon in D2>, no phase shift, amplitude (1/2)
The origins of the √2 and 1/2 terms are a little too complicated to be worth explaining, and come from the math of dealing with multiple photons. (see this paper, or this wikipedia article for a formal treatment).
If we remember from before, interference only occurs in cases where multiple paths lead to the same configuration. This only applies to paths 1 and 4, which both end up in the configuration |photon in D1, photon in D2>. So we add the amplitudes 1/2 and -1/2, which adds to zero amplitude of that state.
After squaring each amplitude, we end up with a 50% chance of finding both photons in D1, a 50% chance of finding both photons in D2, and 0% chance of finding one in each. You either find 2 photons in D1 or D2, but never find them split. This has been experimentally verified!
Now just stop for a second to wrap your head around this. There was destructive interference between the two paths 1 and 4. You can’t decompose this into one part-photon interfering with another part-photon (go ahead, try). The state of the two photons are entangled. What has interfered are two scenarios involving the photons. The scenario of “both reflected” has bumped into “both transmitted”, leaving nothing left.
It doesn’t stop at two photons, though. In principle, every element and property of a system (and possibly the entire universe) can be bundled up into one, universal, extremely high dimensional wavefunction, which can represent every possible combination of properties for every object, including continuous properties like particle position. Every possible configuration of all of the elements of the system will have an amplitude, and we can predict how these amplitudes evolve over time using the Schrodinger equation, a tool that allows us to build up all of chemistry and material science. I cover a bit about the practical applications in this article.
Sensors, collapse, and decoherence
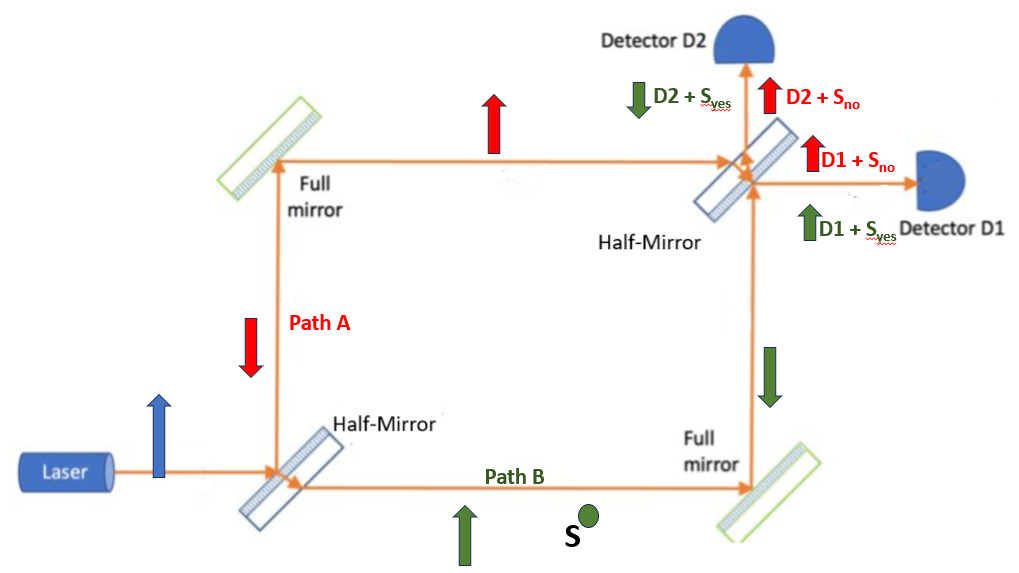
Let’s return back to our interferometer and do one last test. Take our initial test, where all the photons are found in D1. Add a sensor next to the one of the paths, that will return a definite Yes if the photon has gone nearby, and a definite No if the photon hasn’t, without affecting the photon path. Surely this can’t affect the results?
Despite not touching the path of the photons at all, suddenly there will be no interference, and you will see 50% of the time the photon in detector 1, and 50% in detector 2.
One way to think of this is that when the probability amplitude of the part of the photon on path B reaches S, the “wavefunction collapsed”. Instead of being spread between between the two paths, it’s now either 100% in path B and S is “yes”, or 100% in path A and S is “no”. If we think in terms of our arrows, one of the arrows has disappeared, and the other one has stretched out to length 1 to compensate. There is now no “other component” to bounce off of, so there is no interference and 50% detection in each detector. Note that this does not require conscious observation: we don’t need to read the sensor for this change to occur.
A lot of people think this collapse must be some fictional construct like centrifugal force, because it’s acts in ways that are extremely out of line with the other laws of physics (discontinuous, instantaneous, faster than light, etc).
And in fact, we can get rid of the apparent collapse in this scenario. Another way of thinking about the sensor case is that the sensor has become entangled with the photons, and now the configurations arising from each path are distinguishable. Recall that I said that amplitudes add if they lead to the same configuration. But if we include the sensor in our framework, we have different configurations. We have :
0.5 length up arrow amplitude of: |photon in D1 and S says yes>
0.5 length up arrow amplitude of: |photon in D1 and S says no>
0.5 length down arrow amplitude of: |photon in D2 and S says yes>
0.5 length up arrow amplitude of: |photon in D2 and S says no>
They are all different configurations, so no amplitude adding occurs, so the direction of the arrows is once again irrelevant. We get a probability of 0.5^2 = 25% of each outcome, and if we ignore S, we get 50% in D1 and 50% in D2 as predicted. This is the basis of decoherence. The actual theory allows for a lot of little bumps by the environment to have a similar effect.
So, we can see that by taking into account the entanglement of the photon and the sensor, the apparent collapse we saw earlier goes away. Some have theorized that this just keeps going: your measuring equipment gets entangled with S, and then you get entangled with the measuring equipment and S and the photon, so you’ll end up with superpositions of states like:
A: |S says Yes and equipment measures Yes, and You see Yes on the screen>
B: |S says No and equipment measures No, and You see No on the screen>
In this way of thinking (the most commonly told version of many worlds), the You that sees no and the You that sees yes both exist in different worlds, and are both as equally real as the You reading this post. This is an elegant theory, but an incomplete one: we have to explain what it means for the you in state A to have probability 70% and the you in state B to have probability 30%. There have been a lot of attempts to resolve this, but debate is still ongoing as to whether any are likely to be successful. I will have more to say on this in a future article.
On the other hand, if you reject many worlds, you have to explain why entanglement doesn’t go on all the way up to humans, which is also a matter of heated debate. There are a lot of interpretations of quantum mechanics, which all try to replicate reality while biting the least egregious philosophical bullets.
The majority of physicists I know are in the agnostic camp: quantum interpretations may be fun lunchroom conversation, but I already have my hands full with the devilish details of my own problem that is applicable and testable. I’ll just use whatever formalism is easiest to calculate with, and leave the true nature of reality to someone else.
Part 2: Why the math in the sequences is wrong
The reason for writing this up is that a series (1,2,3) of extremely popular blog posts by Eliezer Yudkowsky have covered the same topic, and in my opinion, made a complete mess of it. He covers the same topics I did in this post, but in longer time, making numerous errors, and leaving out important context. They are old, but since they are part of the “sequences” that form the foundational text of the Rationalist movement, they are still read a lot.
In his account, Yudkowsky introduces amplitudes, complex numbers, and the interferometer. The bulk of the error comes when he introduces the half silver mirror with the following description:
Roughly speaking, the half-silvered mirror rule is “multiply by 1 when the photon goes straight, and multiply by i when the photon turns at a right angle.” This is the universal rule that relates the amplitude of the configuration of “a photon going in,” to the amplitude that goes to the configurations of “a photon coming out straight” or “a photon being deflected.”
Remember, the actual half-silver rule (for a single photon) is: transmit one beam forward and reflect one beam 90 degrees, and multiply their amplitudes by 1/√2. If the beam is reflected from the front of the half mirror, also multiply the reflected beam by -1.
The fictional rule is this : transmit one beam forward and reflect one beam 90 degrees. if the beam is reflected (front or back), multiply the amplitude by i.
Up until now, most of the critique has come on this phase shift of i instead of -1, but actually this is actually a fairly minor error. I’m pretty sure a regular half-silver mirror will not do this, but a beamsplitter which induces a phase shift of i on every reflection is theoretically possible, if you carefully engineer a device that induces the correct phase changes on reflection and transmission. You can find plenty of textbooks and online explainers that will use this type of beamsplitter to explain the experiment.
What’s not forgivable is the failure to scale the amplitudes down by 1/√2. By leaving this bit out, this fictional system violates conservation of energy and probability at every half mirror split.
A footnote “correcting” the errors in the post reads:
[Editor’s Note: Strictly speaking, a standard half-silvered mirror would yield a rule “multiply by −1 when the photon turns at a right angle,” not “multiply by i.” The basic scenario described by the author is not physically impossible, and its use does not affect the substantive argument. However, physics students may come away confused if they compare the discussion here to textbook discussions of Mach–Zehnder interferometers. We’ve left this idiosyncrasy in the text because it eliminates any need to specify which side of the mirror is half-silvered, simplifying the experiment.]
Unfortunately, this is also wrong! Firstly, it doesn’t just multiply by -1, it multiplies by -1/√2. And secondly, it only does this when reflecting from the front, not the back. Without that second part, you again violate conservation of energy, and the experiment will pop an extra photon into existence. I think this “correction” is worse than the original text!
There is another major difference between the real system and this fictional one. To get the probability of an amplitude in the real system, we just take the length of the amplitude and we square it, and it spits out the probability of that configuration as is.
In the fictional system, we also square the amplitudes, but because he left out all the scaling factors, we now we sometimes get values over 1. He states we have to renormalize these: if D1 has magnitude squared of 1 and D2 has magnitude squared of 4, then D1 occurs probability 1/5 and D2 occurs probability 4/5.
I think that Yudkowsky might have thought this last change would eliminate the need for keeping track of all the 1/√2 stuff. This is not true, and I will show a few cases where it breaks down.
So, this fictional system is close to reality, except the phase shift acts differently, and the magnitude of each outgoing amplitude doesn’t decrease (violating conservation of energy).
For the specific case of the basic interferometer, this alternate system does gives the same answer as reality. But let me ask you some questions about modifications to our experiment. If you want to check your understanding, try and guess the answers to these questions in the real system. You should have everything you need to figure them out.
What happens if you flip one of the half-mirrors around?
What happens if you replace the bottom full mirror with a half-mirror?
Replace the blocker in the blocker scenario with a third detector as shown below. What are the ratios of photons in each detector?
For change 1: Flipping the half-mirror would mean there was no phase change in path A. The result would be that the photons would be found in detector 2 instead of detector 16. In Yudkowsky’s formalism, the two sides are identical, so nothing would change. This one is a fairly minor critique, easily fixed by changing the words “half silver mirror” to “symmetric beamsplitter”.
For change 2: if you replace one of the full mirrors with half mirrors. in reality, part of the photon would transmit off into space, while another part would reflect and continue on to the detector setup, with both amplitudes reduced by a further 1/√2 factor. Due to this reduced factor, there would only be partial destructive interference: by my calculations, you’d find photons 72.9% of the time in D2, 2.1% in D1, and 25% off in space.
In the fictional system, the amplitude of path B will not be scaled down compared to path A when it hits the extra half-mirror. This means that the portion that heads off to recombine with path A will act the same way it does in the original experiment, leading to amplitude 1 detector 1. The portion that got transmitted off into space would also have amplitude 1, so using the fictional renormalisation rules, you’d see 50% of the photons there, and 50% in detector 1.
Change 3: With the detector 3 acting as a blocker, no interference will occur, so we don’t have to worry about any phase shifts. there is a 1/√2 amplitude going into detector 3, so we square that to get a 50% chance of getting a photon there. Detectors 1 and 2 are symmetrical with amplitude 1/2, so we square that to get a 25% chance of each of them going off.
In the fictional system, the amplitudes have not been scaled. At D3, the amplitude is i, at D2 the amplitude is i, and at D3 the amplitude is -1. So we get probability 1 for finding the photon in D1, and another probability of 1 to find it in D2, and another probability of 1 to find it in D3. Renormalising, we get the incorrect answer that there is an equal 33% chance of finding the photon in each detector.
In all three cases, the fictional system provides inaccurate answers to quite simple modifications.
It’s pretty clear what happened here is that Yudkoswky messed up the math and physics, but didn’t realize it because it gave the right answer, or thought that his “simplifications” wouldn’t affect the results. This is preferable to the alternative, that he knew it was wrong but just didn’t care.
What about the defense that the fictional system is simpler? I think when it comes to the phase shift of i compared to the phase shift of -1, it’s a matter of taste. I prefer my way because it means you only need to keep track of arrow up and arrow down, rather than rotating by 90 degrees every time, and reduces the need to think about complex numbers.
On the other side, not including the 1/√2 factor does simplify things, but at great cost. Because it means that from the first split onwards, we aren’t talking about amplitudes at all. Amplitudes obey the law of conservation of energy and probability, these fictional numbers do not. And this leads to the false predictions we see earlier. It basically means that the reader that learns these rules can’t make accurate predictions with them. It also makes it harder for them to grasp followup posts on deeper questions of interpretations: the scaling of amplitudes is incredibly important when discussing things like the Born rule.
The primary sin of these articles is that they introduce just enough math to be confusing and intimidating to the layman, but not enough to be actually correct or useful. This is the worst of both worlds. Learning this fictional system may almost be detrimental for learning the actual reality, if you don’t realize the problems with it.
The other sin is that a lot of context is left out, so that the layman doesn’t know where to look to get more information. He states that the mirror “multiplies by i”, but if a reader wants to know why this happens, they are in the dark. The word “phase” does not appear once in any of the three articles, despite phase shifts being the main cause of the described effects.
I’m aware that Lesswrong is not meant to be a physics textbook, and that simplification is a necessary part of science communication (I’ve simplified plenty here myself). I really do admire the effort to dive into and communicate how quantum calculations actually operate. But if you’re going to ask people to trust you and to give you their time and attention, you have a responsibility not to tell them the wrong answers. I hope this article goes some way towards rectifying this mistake.
For the origin of these odd brackets, look up “bra ket notation”, or watch this youtube video.
Technically this would be a wavepacket and I’d have to include spatial information of how it’s spread out, but we simplify this for the sake of clarity.
You can also get it to work if the difference in path causes theta to go around an entire circle, so the phase shift of the extra distance is e^i0 = 1 and the phase remains unchanged.
(In reality, you’ll never be this exact with your paths lengths, so you won’t get it down to exactly 0%, but can make it pretty close).
Unless you’re a superdeterminist, but let’s not go down that route.
Actually, this is slightly more complicated if you take into account the thickness of glass. In this case one of the paths would spend more time in the glass of the mirrors of the mirror than the other one, so you’d get additional phase shifts depending on glass thickness which means the result could be anything. This isn’t the case in the regular scenario because it’s symmetrical: both paths spend equal time inside the glass. See here for a more in depth explanation.